5.1 Sampling Variability
If we could repeat the random sampling process, each sample we would get would be slightly different. The composition of units/cases in the sample would differ every time. Sometimes we would randomly over-represent one group of people and another time we would randomly over-represent another group of people, just by chance. The statistic of interest (e.g. a mean, a median, a regression coefficient) that we calculate would vary between across the different samples.
This is one type of random variability. The sample composition can vary, and therefore, the statistics that we calculate vary between different sample.
The important thing to keep in mind is that we only get to see one sample, one particular composition of individuals. But we need to put this one observed sample and statistic in the context of the random variability.
Let’s explore this concept a bit more before we formally talk about probability and chance.
5.1.1 Simulating Random Sampling from a Population
The data set that we will work with contains ALL flights leaving New York City in 2013. This data represents a full census of the target population of flights leaving NYC in a particular year.
We’ll start by creating two new variables, season defined as winter (Oct - March) or summer (April - Sept) and day_hour defined as morning (midnight to noon) or afternoon (noon to midnight).
data(flights)
flights <- flights %>%
na.omit() %>%
mutate(season = case_when(
month %in% c(10:12, 1:3) ~ "winter",
month %in% c(4:9) ~ "summer"
)) %>%
mutate(day_hour = case_when(
between(hour, 1, 12) ~ "morning",
between(hour, 13, 24) ~ "afternoon"
)) %>%
select(arr_delay, dep_delay, season, day_hour, origin, carrier)Since we have the full population of flights in 2013, we could just describe the flights that happened in that year. But, having data on the full population is very rare in practice. Instead, we are going to use this population to illustrate sampling variability.
Let’s take one random sample of 100 flights from the data set, using a simple random sampling strategy.
set.seed(1234) #ensures our random sample is the same every time we run this code
flights_samp1 <- flights %>%
sample_n(size = 100) ## Sample 100 flights randomlyIf you were planning a trip, you may be able to choose between two flights that leave at different times of day. Do morning flights have shorter arrival delays on average than afternoon flights? If so, book the flight earlier in the day!
Let’s look at whether the arrival delay (in minutes) arr_delay differs between the morning and the afternoon, day_hour, by fitting a linear regression model and looking at the estimate for day_hourmorning. This -20.4 minutes is the estimated difference in mean arrival delay times between morning and afternoon flights, so the delay time is less in the morning on average.
## # A tibble: 2 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 14.4 6.38 2.26 0.0258
## 2 day_hourmorning -20.4 10.6 -1.92 0.0578At this point, we haven’t looked at the entire population of flights from 2013. Based on one sample of 100 flights, how do you think the time of day impacts arrival delay times in the entire population?
Now, let’s take another random sample of 100 flights from the full population of flights.
flights_samp2 <- flights %>%
sample_n(size = 100) ## Sample 100 flights randomly
flights_samp2 %>%
with(lm(arr_delay ~ day_hour)) %>%
tidy()## # A tibble: 2 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 3.15 4.46 0.707 0.481
## 2 day_hourmorning -2.11 6.44 -0.328 0.744How does the second sample differ from the first sample? What do they have in common?
We could keep the process going. Take a sample of 100 flights, fit a model, and look at the estimated regression coefficient for day_hourmorning. Repeat many, many times.
We can add a little bit of code to help us simulate this sampling process 1000 times and estimate the difference in mean arrival delay between morning and afternoon for each random sample of 100 flights.
sim_data <- mosaic::do(1000)*(
flights %>%
sample_n(size = 100) %>% # Generate samples of 100 flights
with(lm(arr_delay ~ day_hour)) # Fit linear model
)Now we have 1000 fit models, each corresponding to one random sample of 100 flights from the population. Let’s summarize and visualize this simulation.
# Summarize
sim_data %>%
summarize(
mean_Intercept = mean(Intercept),
mean_dayhourmorning = mean(day_hourmorning),
sd_Intercept = sd(Intercept),
sd_dayhourmorning = sd(day_hourmorning))## mean_Intercept mean_dayhourmorning sd_Intercept sd_dayhourmorning
## 1 13.45053 -14.54158 7.233256 8.87308# Visualize Intercepts
sim_data %>%
ggplot(aes(x = Intercept)) +
geom_histogram(bins = 15) +
labs(title = "Sampling distribution of Intercepts\nfrom samples of 100 flights") +
theme_minimal()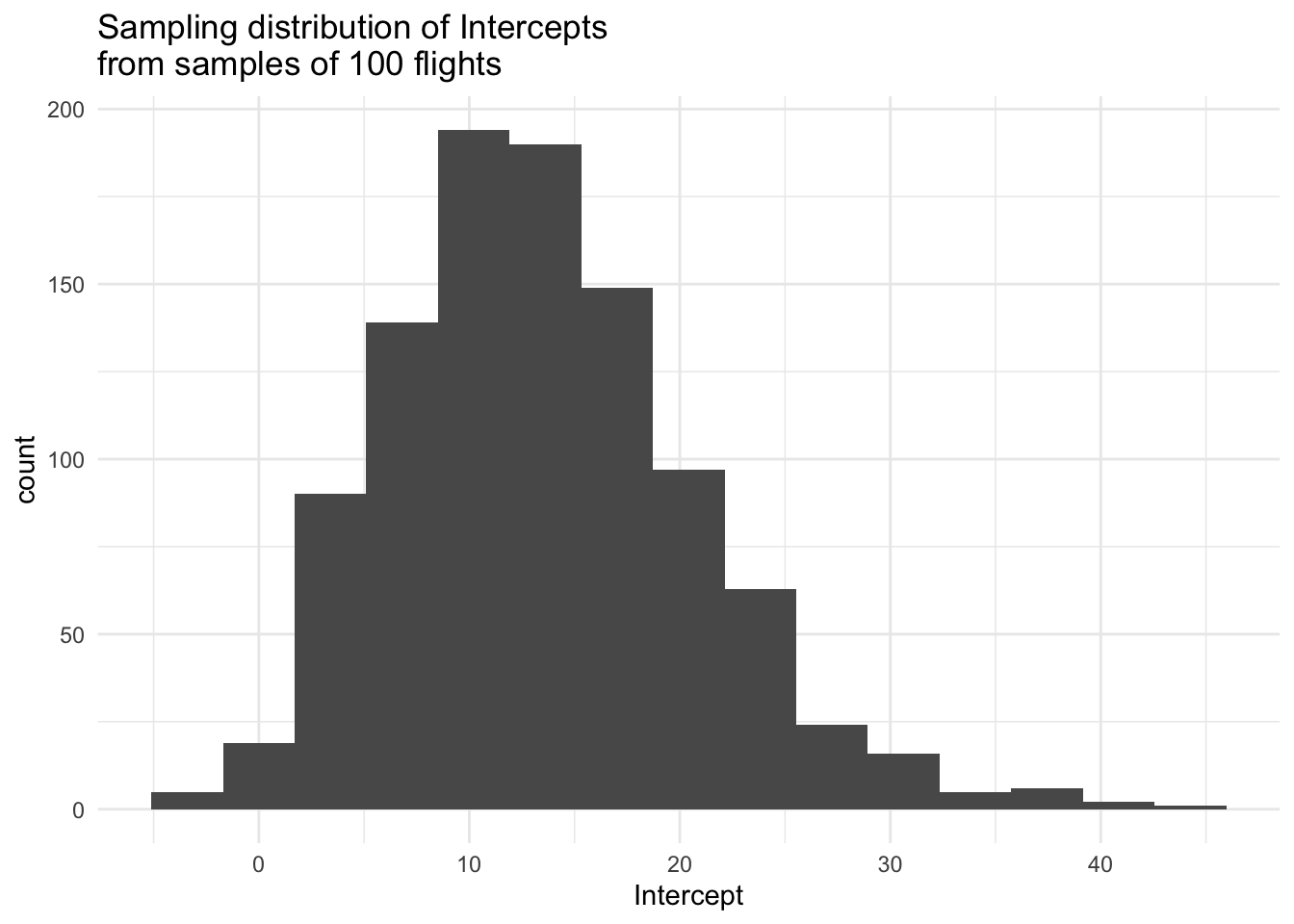
# Visualize Slopes
sim_data %>%
ggplot(aes(x = day_hourmorning)) +
geom_histogram(bins = 15) +
labs(title = "Sampling distribution of Slopes\nfrom samples of 100 flights") +
theme_minimal()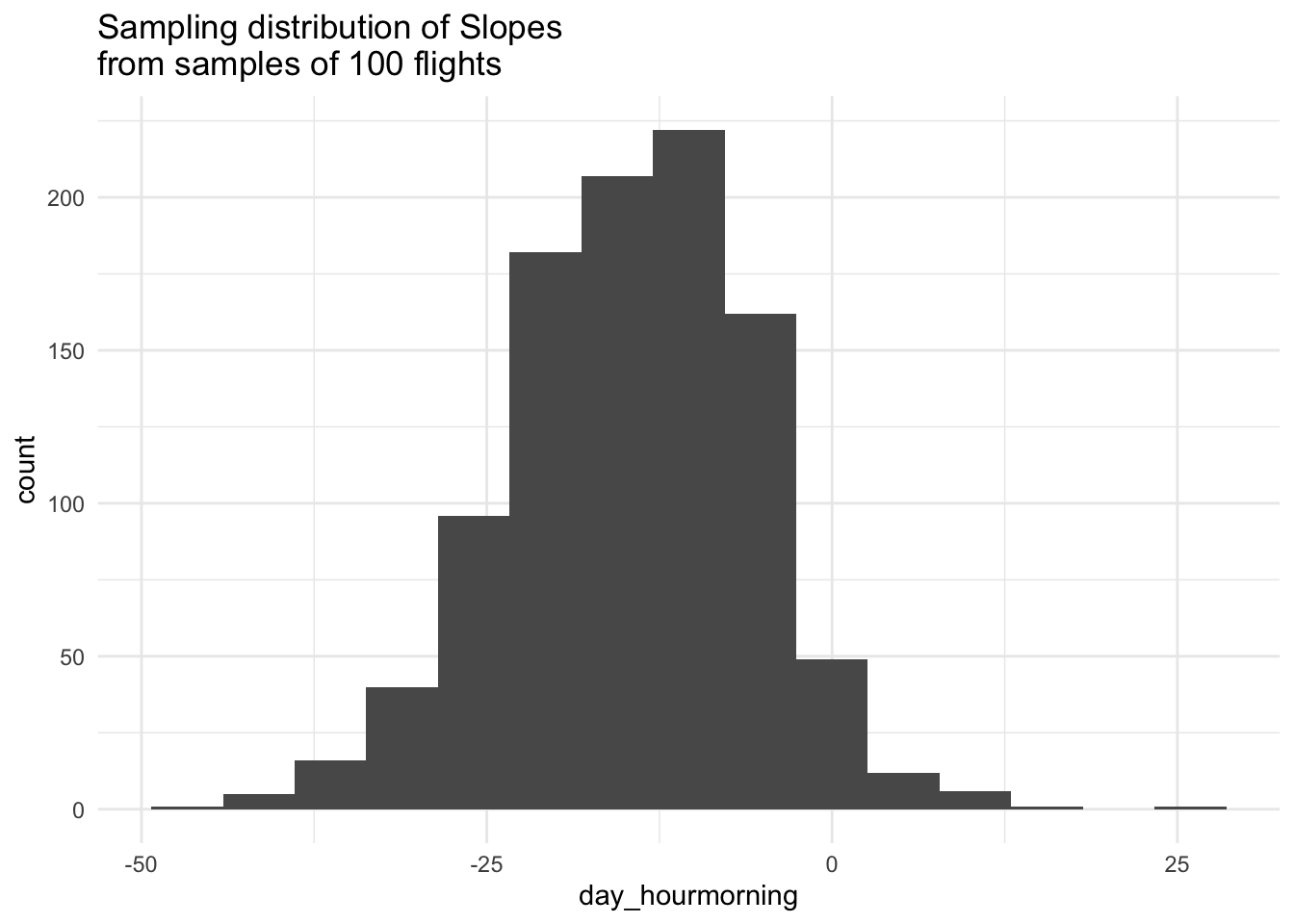
These histograms approximate the sampling distribution of estimated intercepts and the sampling distribution of estimated slopes from a linear model predicting the arrival delay as a function of time of day, both of which describe the variability in the sample statistics across all possible random samples from the population.
Describe the shape, center, and spread of the sampling distribution for the intercepts. Do the same for the slopes.
Notice how these means of the sampling distributions are very close to the population values, below. This makes sense since we are sampling from the population so we’d expect the estimates to bounce around the true population values.
sim_data %>% # Means and standard deviations of sampling distribution
summarize(
mean_Intercept = mean(Intercept),
mean_dayhourmorning = mean(day_hourmorning),
sd_Intercept = sd(Intercept),
sd_dayhourmorning = sd(day_hourmorning))## mean_Intercept mean_dayhourmorning sd_Intercept sd_dayhourmorning
## 1 13.45053 -14.54158 7.233256 8.87308##
## Call:
## lm(formula = arr_delay ~ day_hour)
##
## Coefficients:
## (Intercept) day_hourmorning
## 13.42 -14.605.1.2 IRL: Bootstrapping
In real life (IRL), we don’t have a full target population from which we can repeatedly draw samples. We only have one sample that was already drawn from the larger target population.
To get a sense of the sampling variability, we could try to mimic this process of sampling from the full target population using our best stand-in for the population: our sample. We will call the sample our “fake population” for the moment. This process of resampling our sample is called bootstrapping.
We bootstrap our sample in order to 1) estimate the variability of the statistic and 2) get a range of plausible values for the true population parameter.
There are four steps to bootstrapping. They are very similar to simulating the sampling process from a population.
1. Generate
To generate different random samples of the same size (100 flights) from our “fake population”, we have to draw sample of 100 flights WITH REPLACEMENT, meaning that we have to put a flight back into the pool after drawing them out.
What would happen if we drew WITHOUT REPLACEMENT?
2. Calculate
In our simulation above, we calculated the median and mean arrival delay. In theory, we could calculate any numerical summary of data (e.g. the mean, median, SD, 25th percentile, etc.)
boot_data <- mosaic::do(1000)*(
flights_samp1 %>% # Start with the SAMPLE (not the FULL POPULATION)
sample_frac(replace = TRUE) %>% # Generate by resampling with replacement
with(lm(arr_delay ~ day_hour)) # Fit linear model
)Notice the similarities and differences in the R code for boot_data, in which we are sampling from the sample, and sim_data, in which we are sampling from the population, above.
3. Summarize
Let’s summarize these 1000 model estimates generated from resampling (with replacement) from our sample (our “fake population”).
# Summarize
boot_data %>%
summarize(
mean_Intercept = mean(Intercept),
mean_dayhourmorning = mean(day_hourmorning),
sd_Intercept = sd(Intercept),
sd_dayhourmorning = sd(day_hourmorning))## mean_Intercept mean_dayhourmorning sd_Intercept sd_dayhourmorning
## 1 14.58742 -20.49495 7.218149 8.44133Note how the mean’s are very close to the original estimates from the sample, below.
## # A tibble: 2 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 14.4 6.38 2.26 0.0258
## 2 day_hourmorning -20.4 10.6 -1.92 0.0578This is not a coincidence. Since we are resampling from our original sample, we’d expect the bootstrap estimates to bounce around the original sample estimates, similar to how the simulated sampling distributions had means close the the population values
Let’s compare this to the summaries from the simulation of randomly sampling from the population.
sim_data %>%
summarize(
mean_Intercept = mean(Intercept),
mean_dayhourmorning = mean(day_hourmorning),
sd_Intercept = sd(Intercept),
sd_dayhourmorning = sd(day_hourmorning))## mean_Intercept mean_dayhourmorning sd_Intercept sd_dayhourmorning
## 1 13.45053 -14.54158 7.233256 8.87308The means won’t be exactly the same because the center of the bootstrap distribution is the original sample and the center of the sampling distribution is the population values.
But, the standard deviations should be of roughly similar magnitude because they are in fact trying to estimate the same thing, the sampling variability.
4. Visualize
Let’s visualize these 1000 models generated from resampling (with replacement) from our sample (our “fake population”).
# Visualize Intercepts
boot_data %>%
ggplot(aes(x = Intercept)) +
geom_histogram(bins = 15) +
labs(title = "Bootstrap sampling distribution of Intercepts\nfrom samples of 100 flights") +
theme_minimal()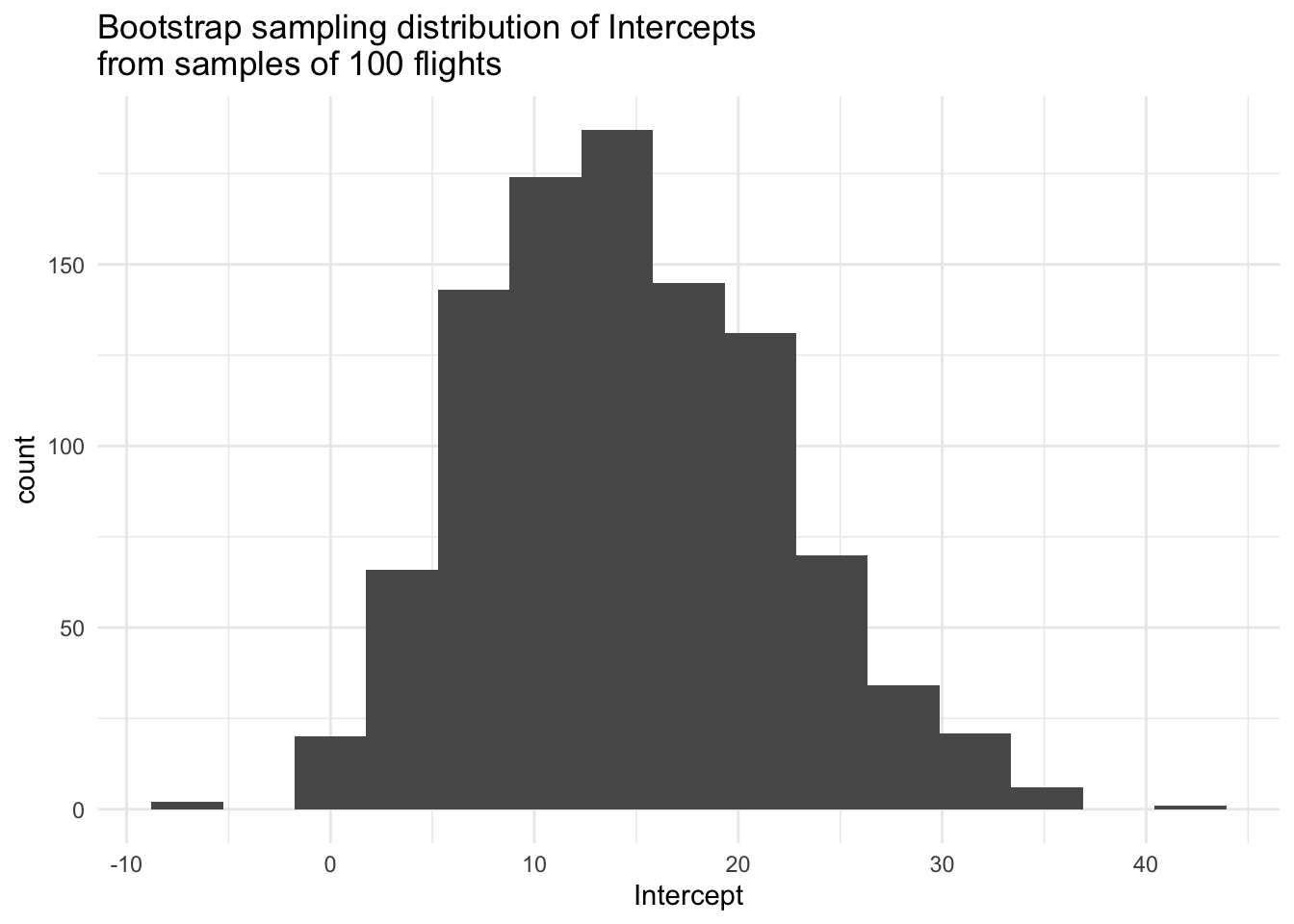
# Visualize Slopes
boot_data %>%
ggplot(aes(x = day_hourmorning)) +
geom_histogram(bins = 15) +
labs(title = "Bootstrap sampling distribution of Slopes\nfrom samples of 100 flights") +
theme_minimal()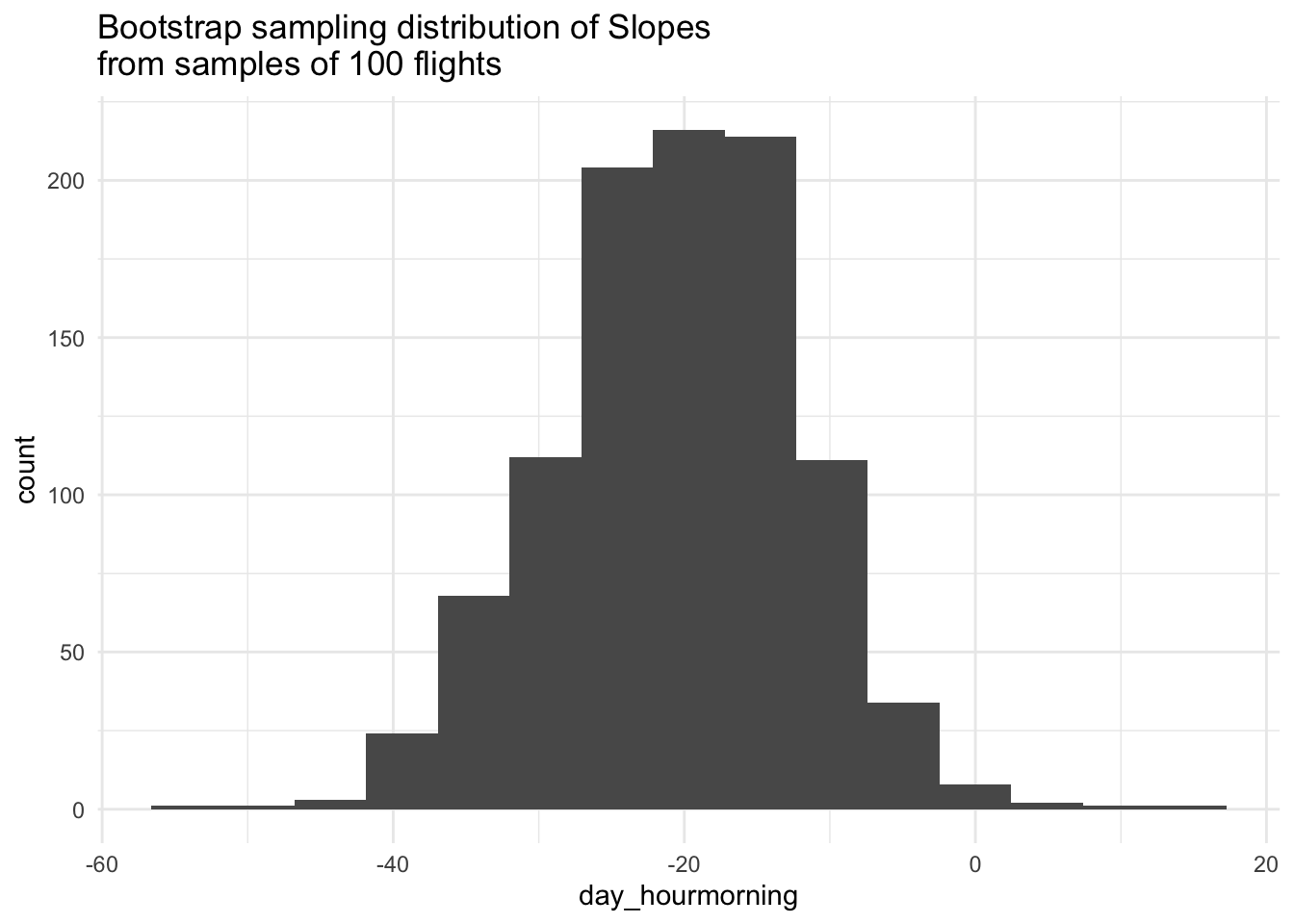
Let’s compare these to the visuals from the simulation from the population.
# Visualize Intercepts
sim_data %>%
ggplot(aes(x = Intercept)) +
geom_histogram(bins = 15) +
labs(title = "Sampling distribution of Intercepts\nfrom samples of 100 flights") +
theme_minimal()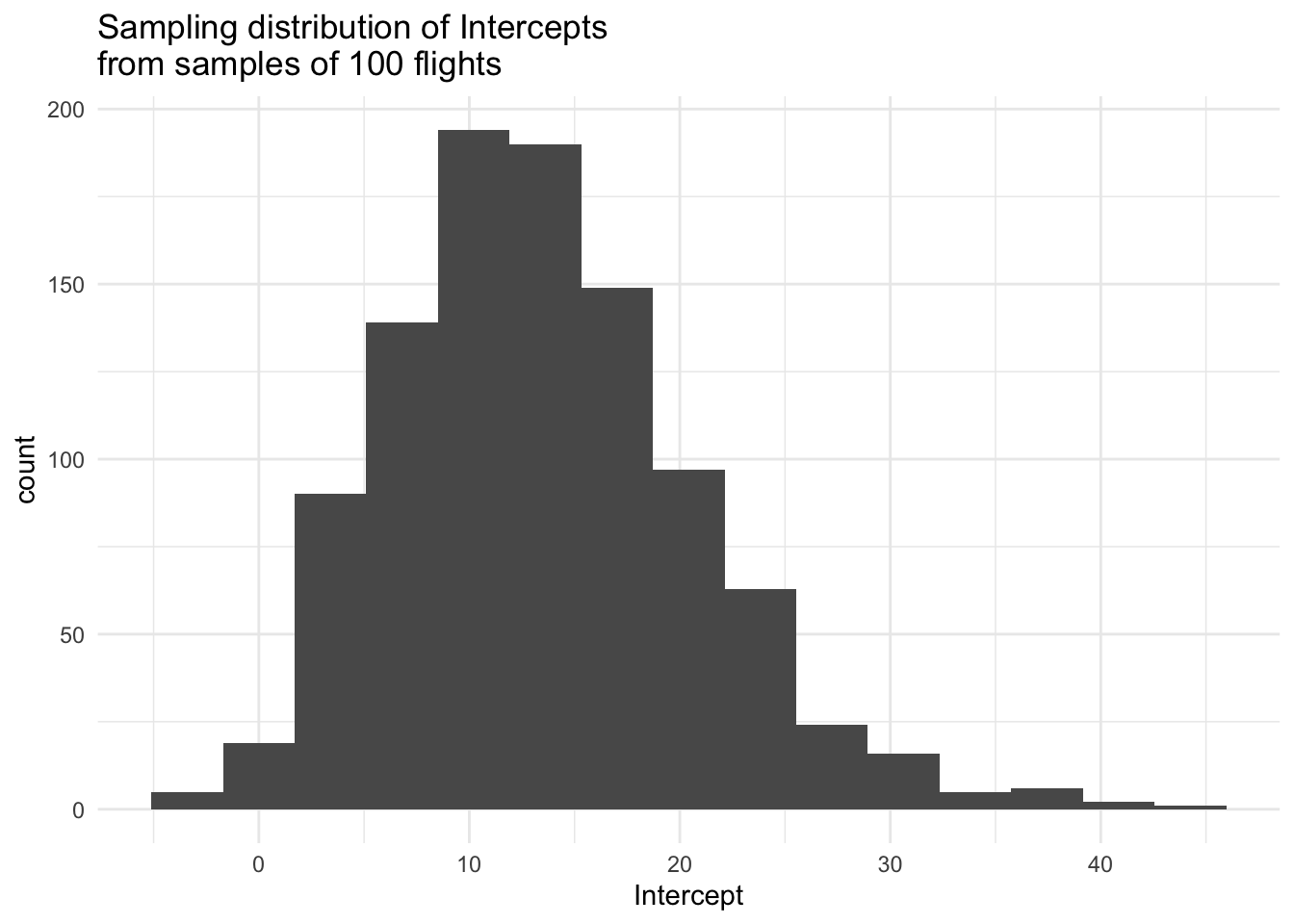
# Visualize Slopes
sim_data %>%
ggplot(aes(x = day_hourmorning)) +
geom_histogram(bins = 15) +
labs(title = "Sampling distribution of Slopes\nfrom samples of 100 flights") +
theme_minimal()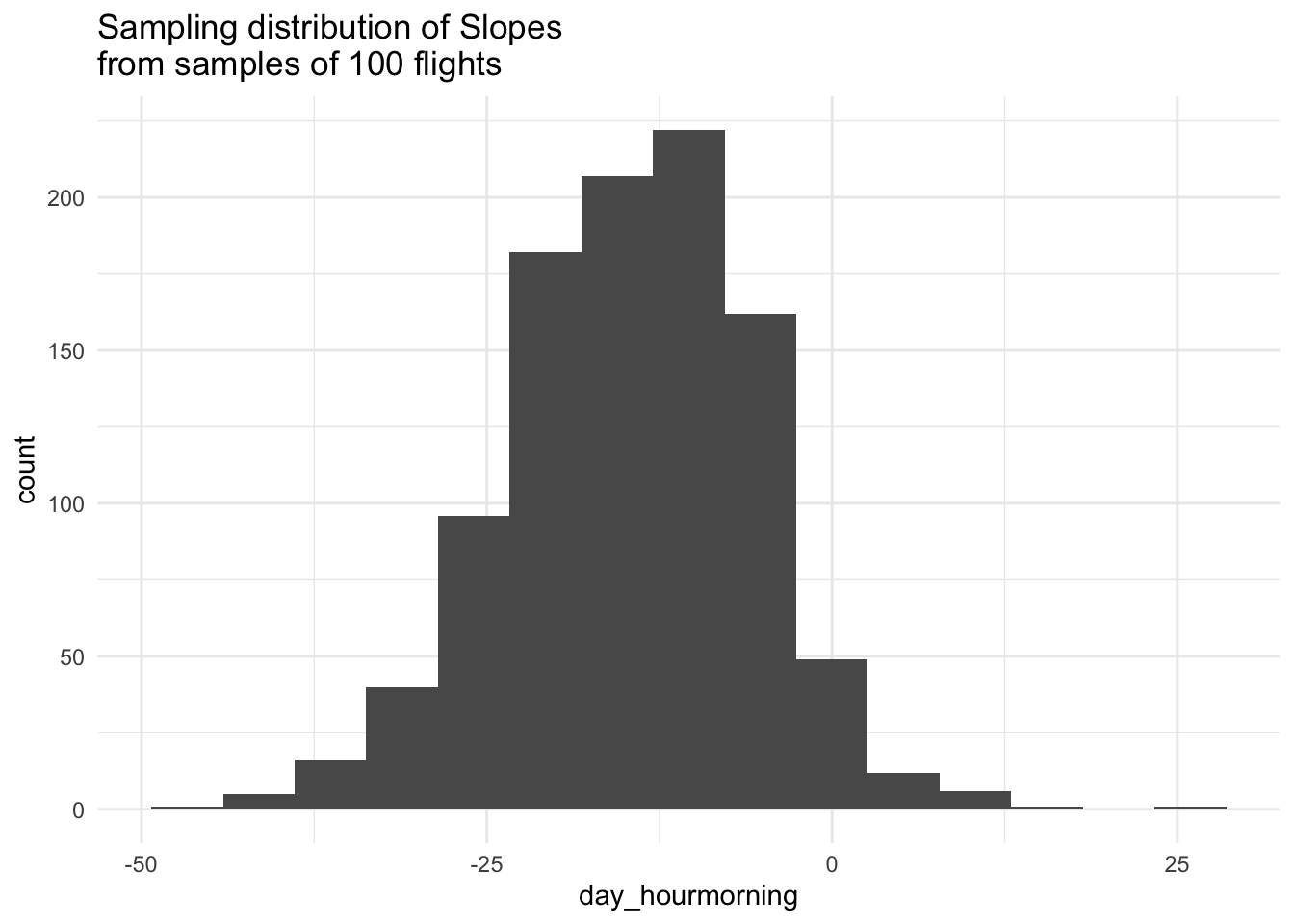
The process of resampling from our sample, called bootstrapping, is becoming the one of main computational tools for estimating sampling variability in the field of Statistics.
How well does bootstrapping do in mimicking the simulations from the population? What could we change to improve bootstrap’s ability to mimic the simulations?
This is a really important concept in Statistics! We’ll come back to the ideas of sampling variability and bootstrapping throughout the rest of the course.
Based on the bootstrap sampling distribution, what would you guess the difference in mean arrival delay between morning and afternoon is in the population of flights?
Based on the bootstrap sampling distribution, if you had to give an interval of plausible values for the population difference, what range would you give? Why? Is a difference of 0 a plausible value?