4.1 Logistic and Logit

Since we can’t use a straight line model, we’ll need to consider other mathematical functions to model the relationship between \(X\) and the chance of success, \(p=E[Y]\).

The logistic function is an S shaped curve (sigmoid curve). For our purposes, the function will take the form

\[f(x) = \frac{1}{1 + e^{\beta_0 +\beta_1x}}\]

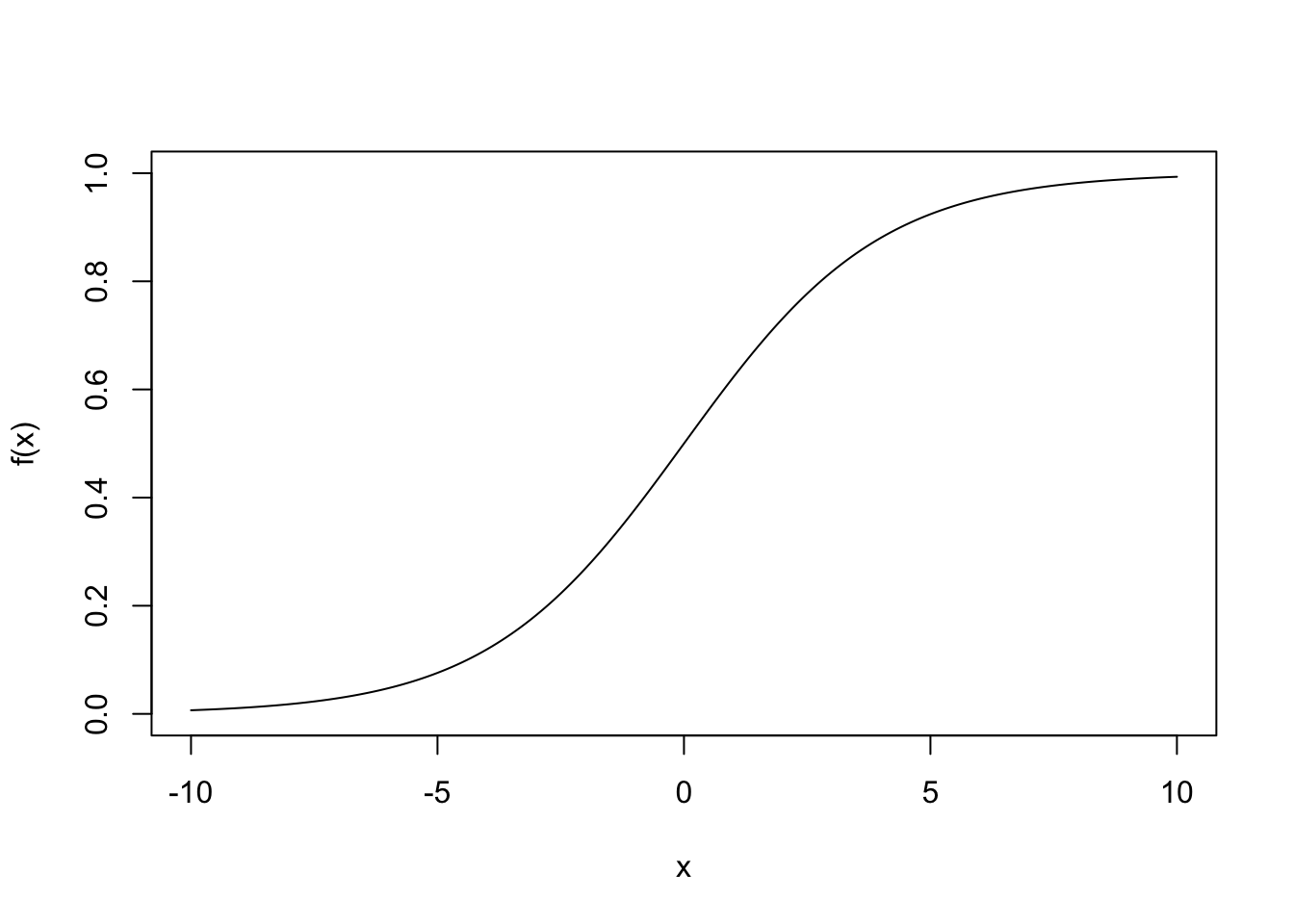
For any real value \(x\), this function, \(f(x)\), will be a value between 0 and 1. This is perfect for us since probabilities or chances should also be between 0 and 1.

In fact, we’ll let the chance of failure outcome (when \(Y=0\)), \(1-p\), be modeled by this S function.

\[1-p = \frac{1}{1 + e^{\beta_0 +\beta_1X}}\]

With a bit of algebra and rearranging terms, we can write this equation in terms of \(p\), the chance of success.

\[1-p = \frac{1}{1 + e^{\beta_0 +\beta_1X}}\] \[p = 1-\frac{1}{1 + e^{\beta_0 +\beta_1X}}\]

\[p = \frac{1 + e^{\beta_0 +\beta_1X}}{1 + e^{\beta_0 +\beta_1X}}-\frac{1}{1 + e^{\beta_0 +\beta_1X}}\]

\[p = \frac{e^{\beta_0 +\beta_1X}}{1 + e^{\beta_0 +\beta_1X}}\]

Let’s define one more term. The odds of a success is the ratio of the chance of success to the chance of failure, odds \(=p/(1-p)\).

With a bit more algebra and rearranging terms, we can write the above model as a linear regression model.

\[p/(1-p) = \frac{e^{\beta_0 +\beta_1X}}{1 + e^{\beta_0 +\beta_1X}}/\frac{1}{1 + e^{\beta_0 +\beta_1X}}\] \[p/(1-p) = e^{\beta_0 +\beta_1X}\] \[\log(p/(1-p)) = \beta_0 +\beta_1X\]

This is a simple logistic regression model. On the left hand side, we have the natural log of the odds of success for a given value of \(X\). The log odds is called the logit function. Think of this as a transformed version of our expected outcome for a given value of \(X\). On the right hand side, we have a familiar linear model equation.

\[\log\left(\frac{p}{1-p}\right) =\log\left(\hbox{Odds of Success given } X\right) = \log\left(\frac{E[Y|X]}{1-E[Y|X]}\right) = \beta_0 +\beta_1X\]

Like a linear regression model, we can extend this model to a multiple logistic regression model by adding additional \(X\) variables,

\[\log\left(\frac{p}{1-p}\right) =\log\left(\hbox{Odds of Success given } X_1,...,X_k\right)= \log\left(\frac{E[Y|X_1,...,X_k]}{1-E[Y|X_1,...,X_k]}\right) \\ = \beta_0 +\beta_1X_1+\beta_2X_2+\beta_3X_3+\cdots +\beta_kX_k\]