3.11 Causal Inference
A full overview of causal inference is beyond the scope of this course, but a first good step in this direction is to consider a causal model, which is a representation of the causal mechanism by which data were generated. We typically visualize these models with a graphical structure called a directed acyclic graph or DAG for short.
In a DAG, we have circles or nodes that represented variables and arrow or directed edges that indicate the causal pathway (arrows point in the direction of the hypothesized casual effect).
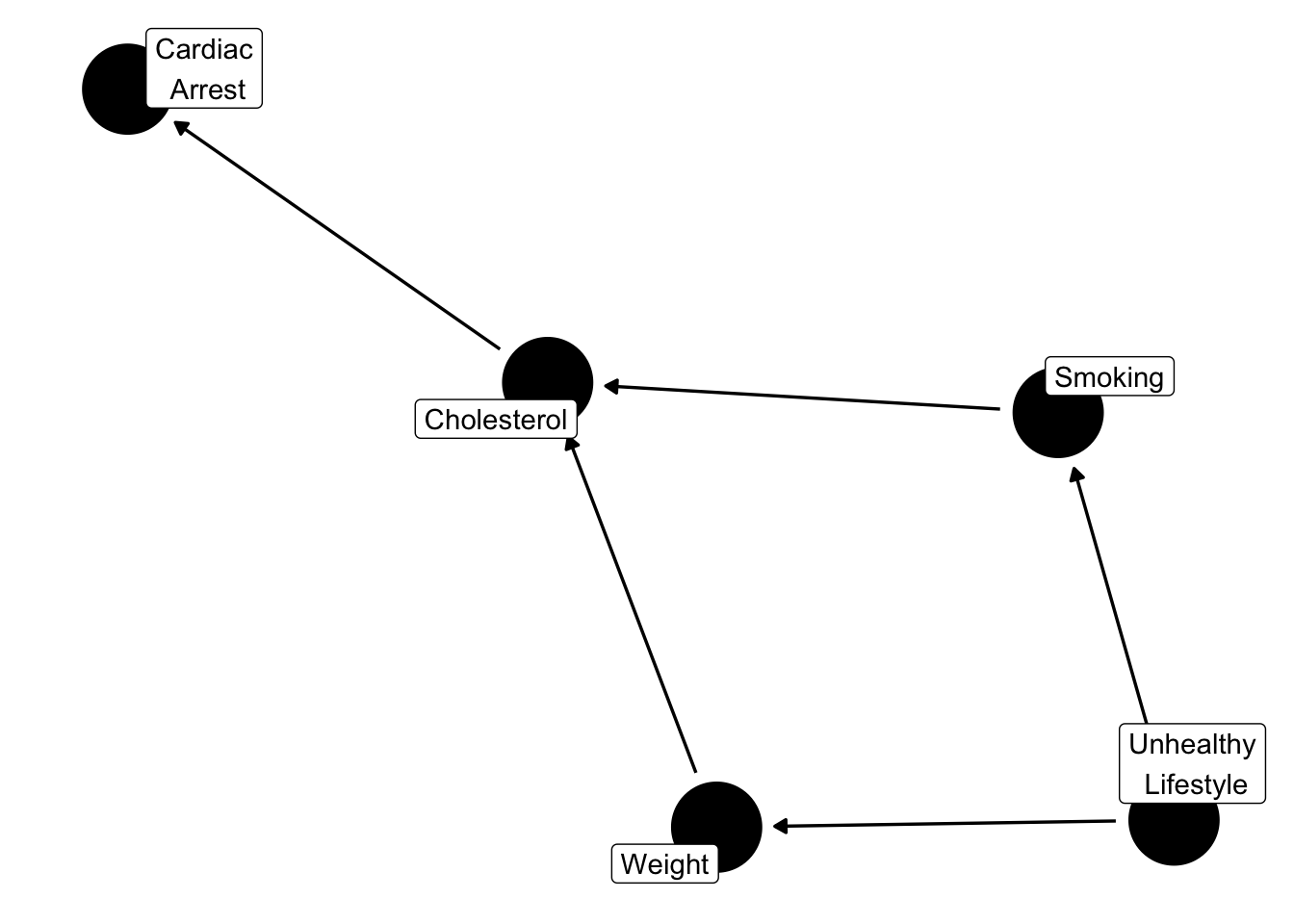
Below we discuss the three basic DAG structures.
Chain: A chain includes three nodes and two edges, with one directed into and one edge directed out of the middle variable. In the above example, we see a few chains. There is a chain that suggests an unhealthy lifestyle leads to smoking which directly impacts cholesterol levels. Another chain suggests an unhealthy lifestyle direclty impacts human weight which impacts cholesterol levels. By our DAG, there are two causal pathways that directly impact cholesterol levels.
Fork: A fork includes three nodes with two arrows emanating from the middle variable. The only fork in the example above involves unhealthy lifestyle (middle variable), weight, and smoking. In this case, we are assuming that an unhealthy lifestyle is a common cause of both weight and smoking. Thus, the lifestyle might confound the relationship between smoking and weight, in that smoking and weight may appear to be associated with each other because they have a common cause.
Colliders: A collider occurs when one node receives edges from two other nodes. In the example above, smoking and weight have a common effect, cholesterol.
These structures are important to understand because they can help guide our analysis and modeling. Assuming the causal model is correct (which might not be…), we have a better sense of how smoking might be related to cardiac arrest.
- There is a direct path from smoking through cholesterol to cardiac arrest. Smokers may have a higher cholesterol level and thus a higher risk of cardiac arrest.
- There is an indirect (backdoor) path from smoking to cardiac arrest through weight. Smokers also have an unhealty lifestyle which means they are likely to have a higher weight leading to a higher cholesterol level and thus a higher risk of cardiac arrest.
If we only want to estimate the direct relationship between smoking and cardiac arrest, we need to block the impact of the indirect path. We alluded earlier that multiple linear regression could provide estimates of causal effects in the right circumstances. What are those circumstances? When we include all confounding variables in the model.
Remember, a confounder is a common cause of both the causal variable of interest and the outcome (e.g. living area could be a confounder of fireplace presence and house price).
However, we should not just throw every variable we have into a multiple regression model. Why? Imagine a scenario for understanding how smoking affects lung cancer development. It is very important to consider whether a variable is a mediator of the relationship between the cause and the outcome. A mediator is a variable in a chain or along the path between the cause and the outcome. In the smoking and lung cancer example, one mediator could be tar in the lungs. Suppose that smoking only affects lung cancer risk by creating tar on the lungs. If we adjust for tar (by holding it constant), then we also effectively hold smoking constant too! If smoking is held constant, then we cannot estimate its effect on cancer risk because it is not varying!
Wait - we could never possibly know of or measure all confounding variables, could we!? This is true, but that doesn’t mean that our endeavor to understand causation is fruitless. As long as we can describe the relationship between known confounders as precisely as possible with writing down a DAG (causal model), we have a starting ground for moving forward.
We collect data, analyze how well our model predicts that data, and collect more data based on that, perhaps measuring more potential confounders as our scientific knowledge grows. We can also conduct sensitivity analyses by asking: how strongly must a confounder affect the variable of causal interest and the outcome to completely negate or reverse the association we see? Such endeavors and more are the subject of the field of causal inference.
Multiple linear regression offers us a way to estimate causal effects of variables if we use it carefully. It will be tempting to say: include every variable we can! But we will see that this is not the correct thing to do, as there are very real dangers of over-controlling for variables (known as throwing everything in the model). For now, let it suffice to say that multiple linear regression is as useful as the corn kerneler below. Immensely useful in the right circumstances - but only those circumstances.

If you want a “gentle” but mathematical introduction to Causal Inference, we suggest taking the class at Macalester and/or reading “Causal Inference in Statistics: A Primer” by Judea Pearl, Madelyn Glymour, Nicholas P. Jewell). Fun Fact: Nicholas Jewell was Prof. Heggeseth’s PhD advisor!